线性神经网络

yczha大约 5 分钟

摘要

这篇文章我们介绍线性神经网络，包括线性回归模型和softmax模型。

线性回归

公式推导

对于n个特征的样本，线性方程表示为：

\hat{y} = w_{1} x_{1} + w_{2} x_{2} + . . . + w_{n} x_{n} + b

上式可以用向量简化表示为：

\hat{y} = \vec{w^{T}} \vec{x} + b

对于有m个样本的数据集，进一步用矩阵表示为：

\hat{y} = X w + b

损失函数

我们用损失函数来表示拟合结果跟实际值之间的差距。回归问题中常用的损失函数是平方误差：

l^{(i)} (w, b) = \frac{1}{2} ({\hat{y}}^{(i)} - y^{(i)})^{2}

由于平方误差函数中的二次方项，估计值 ${\hat{y}}^{(i)}$ 和观测值 $y^{(i)}$ 之间较大的差异将导致更大的损失。为了度量模型在整个数据集上的质量，我们需计算在训练集m个样本上的损失均值：

L (w, b) = \frac{1}{m} \sum_{i = 1}^{m} l^{(i)} (w, b) = \frac{1}{m} \sum_{i = 1}^{m} \frac{1}{2} (w^{T} x^{(i)} + b - y^{(i)})^{2}

在训练模型时，我们希望寻找一组参数 $(w^{*}, b^{*})$ ，这组参数能最小化在所有训练样本上的总损失。如下式：

w^{*}, b^{*} = \underset{w, b}{a r g m i n} L (w, b)

解析解

线性回归刚好是一个很简单的优化问题，ta的解可以用一个公式简单地表达出来，我们的预测问题是最小化 $‖ y - X w ‖^{2}$ 。这在损失平面上只有一个临界点，这个临界点对应于整个区域的损失极小点。将损失关于 $w$ 的导数设为0，得到解析解：

w^{*} = (X^{T} X)^{- 1} X^{T} y

随机梯度下降

深度学习中的大部分场景都没办法求得解析解，这时候可以使用梯度下降法来求解。梯度下降法可以用公式表示为：

(w, b) \leftarrow (w, b) - η * \partial_{(w, b)} L (w, b)

实际应用中，如果对整个数据集进行更新，往往计算量过大，此时可以随机选择一个小批次数据集 $β$ （batch）进行更新，称为随机梯度下降：

(w, b) \leftarrow (w, b) - \frac{η}{β} * \sum_{β} \partial_{(w, b)} L (w, b)

从零实现性线回归

准备数据集

为了进行模型训练和验证，我们先来准备一份模拟数据集

"""
生成线性回归数据集
"""

import torch
from torch.utils import data


class Dataset(data.Dataset):
    """生成数据"""
    def __init__(self, num_samples=1000, num_features=10):
        super().__init__()
        self.num_samples = num_samples
        self.num_features = num_features
        self.true_w = torch.tensor(range(1, num_features+1))
        self.true_b = torch.tensor(1)
        self.dataset, self.gt = self._gen_data()

    def _gen_data(self):
        X = torch.normal(0, 1, (self.num_samples, self.num_features))
        y = X @ self.true_w.float() + self.true_b.float()
        y += torch.normal(0, 0.01, y.shape)
        return X, y.reshape((-1, 1))
    
    def __len__(self):
        return self.num_samples
    
    def __getitem__(self, index):
        return self.dataset[index], self.gt[index]


def show_data(dataset):
    """
    可视化数据
    """
    import matplotlib.pyplot as plt
    n = len(dataset)
    features = [dataset[i][0][-1] for i in range(n)]
    gt = [dataset[i][1][0] for i in range(n)]

    plt.scatter(features, gt, s=2)
    plt.show()


if __name__ == "__main__":
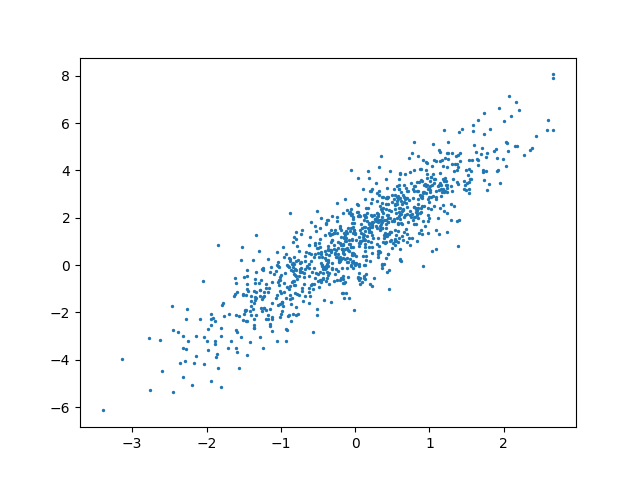
    dataset = Dataset(num_samples=1000, num_features=2)
    show_data(dataset)

查看一下数据集：

实现代码

接下来我们实现模型代码

import torch
import torch.nn as nn
from torch.utils import data

from gen_linear_regression_dataset import Dataset


class LRModel(nn.Module):
    """
    线性模型实现
    """
    def __init__(self, num_features):
        super().__init__()
        self.w = torch.normal(0, 0.01, size=(num_features, 1), requires_grad=True)
        self.b = torch.zeros(1, requires_grad=True)

    def forward(self, X):
        return torch.matmul(X, self.w) + self.b


def squared_loss(y_hat, y):
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2


def sgd(params, lr, batch_size):
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()


def train():    
    # 模型超参数
    lr = 0.01
    num_epochs = 10
    batch_size = 10
    num_features = 2
    # 初始化模型
    model = LRModel(num_features)
    # 数据集加载器
    dataset = Dataset(num_samples=1000, num_features=num_features)
    dataloader = data.DataLoader(dataset, batch_size=batch_size, shuffle=True, num_workers=0)
    # 迭代训练
    for epoch in range(num_epochs):
        loss_batch = []
        for X, y in dataloader:
            y_hat = model(X)
            loss = squared_loss(y_hat, y)
            loss.sum().backward()
            sgd([model.w, model.b], lr, batch_size)
            loss_batch.append(loss.sum().item()) 
        print(f'epoch {epoch + 1}, loss {torch.tensor(loss_batch).mean().item():>.4f}')

    # 校验结果
    print("模型拟合的参数：", model.w.detach().numpy().tolist(), model.b.detach().numpy().tolist())
    print("真实情况的参数：", dataset.true_w.numpy(), dataset.true_b.numpy())


if __name__ == "__main__":
    train()

运行结果如下：

epoch 1, loss 13.0411
epoch 2, loss 1.6455
epoch 3, loss 0.2089
epoch 4, loss 0.0270
epoch 5, loss 0.0039
epoch 6, loss 0.0009
epoch 7, loss 0.0006
epoch 8, loss 0.0005
epoch 9, loss 0.0005
epoch 10, loss 0.0005

最后我们来看一下训练效果如何：

模型拟合的参数： [[0.9998961091041565], [1.9998223781585693]] [1.0004650354385376]
真实情况的参数： [1 2] 1

可见拟合很接近真实值！

简化实现

接下来我们使用torch自带的函数来简化模型的实现：

import torch
import torch.nn as nn
from torch.utils import data

from gen_linear_regression_dataset import Dataset


class LRModel(nn.Module):
    """线性模型简化实现"""
    def __init__(self, num_features):
        super().__init__()
        self.net = nn.Sequential(nn.Linear(num_features, 1))
        # 初始化参数
        self.net[0].weight.data.normal_(0, 0.01)
        self.net[0].bias.data.fill_(0)

    def forward(self, X):
        return self.net(X)
    

def train():    
    # 模型超参数
    lr = 0.01
    num_epochs = 10
    batch_size = 10
    num_features = 2
    # 初始化模型
    model = LRModel(num_features)
    # 数据集加载器
    dataset = Dataset(num_samples=1000, num_features=num_features)
    dataloader = data.DataLoader(dataset, batch_size=batch_size, shuffle=True, num_workers=0)
    # 损失函数
    loss_fn = nn.MSELoss()
    # 优化器
    sgd = torch.optim.SGD(model.parameters(), lr)
    # 迭代训练
    for epoch in range(num_epochs):
        loss_batch = []
        for X, y in dataloader:
            y_hat = model(X)
            loss = loss_fn(y, y_hat)
            sgd.zero_grad()
            loss.backward()
            sgd.step()
            loss_batch.append(loss.sum().item())
        print(f'epoch {epoch + 1}, loss {torch.tensor(loss_batch).mean().item():>.4f}')

    # 校验结果
    print("模型拟合的参数：", model.net[0].weight.detach().numpy().tolist(), model.net[0].bias.detach().numpy().tolist())
    print("真实情况的参数：", dataset.true_w.numpy(), dataset.true_b.numpy())


if __name__ == "__main__":
    train()

看一下效果：

模型拟合的参数： [[0.9992117881774902, 2.000218152999878]] [0.9992788434028625]
真实情况的参数： [1 2] 1

Softmax 回归

基础概念

线性回归可以用来解决回归问题，对于分类问题，我们需要探索不同的方法。

社会科学家邓肯·卢斯于1959年在选择模型（choice model）的理论基础上发明了softmax函数，该函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质。该函数公式如下：

\hat{y} = s o f t m a x (o), 其中 {\hat{y}}_{j} = \frac{e x p (o_{j})}{\sum_{k} e x p (o_{k})}

尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。因此，softmax回归是一个线性模型。

损失函数

对于给定样本集 ${X, Y}$ ，我们的目标是使得总的概率最大化：

P (Y | X) = \prod_{i = 1}^{n} P (y^{(i)} | x^{(i)})

根据最大似然估计，我们最大化 $P (Y | X)$ ，相当于最小化负对数似然：

- l o g P (Y | X) = \sum_{i = 1}^{n} - l o g P (y^{(i)} | x^{(i)}) = \sum_{i = 1}^{n} l (y^{(i)}, {\hat{y}}^{(i)})

其中，对于任何标签 $y$ 和模型预测 $\hat{y}$ ，损失函数为：

l (y, \hat{y}) = - \sum_{j = 1}^{q} y_{j} l o g \hat{y}

该损失函数通常被称为交叉熵损失。y是一个长度为q的独热编码向量。

将 $\hat{y}$ 的表达式带入，上式可得：

l (y, \hat{y}) = - \sum_{j = 1}^{q} y_{j} l o g \hat{y} = - \sum_{j = 1}^{q} y_{j} l o g \frac{e x p (o_{j})}{\sum_{k = 1}^{q} e x p (o_{k})} = \sum_{j = 1}^{q} y_{i} l o g \sum_{k = 1}^{q} e x p (o_{k}) - \sum_{j = 1}^{q} y_{j} o_{j} = l o g \sum_{k = 1}^{q} e x p (o_{k}) - \sum_{j = 1}^{q} y_{j} o_{j}

进一步，损失函数的导数得：

\partial_{o_{j}} l (y, \hat{y}) = \frac{e x p (o_{j})}{\sum_{j = 1}^{q} e x p (o_{j}) - y_{j}} = s o f t m a x (o)_{j} - y_{j}

从零实现softmax回归

数据集准备

为了完成模型的验证，我们需要先准备一份数据集。这里选择Fashion-MNIST，该数据集由10个类别的图像组成，每个类别由训练数据集（train dataset）中的6000张图像和测试数据集（test dataset）中的1000张图像组成。因此，训练集和测试集分别包含60000和10000张图像。测试数据集不会用于训练，只用于评估模型性能。

首先下载数据：

import pathlib

import torch
import torchvision
from torchvision import transforms
from torch.utils import data

proj_dir = str(pathlib.Path(__file__).parent)


def download_dataset():
    """下载数据集"""
    trans = transforms.ToTensor()
    fashion_mnist_train = torchvision.datasets.FashionMNIST(root=proj_dir, train=True, download=True, transform=trans)
    fashion_mnist_test = torchvision.datasets.FashionMNIST(root=proj_dir, train=False, download=True, transform=trans)
    return fashion_mnist_train, fashion_mnist_test


def show_images(imgs, num_rows, num_cols, titles=None, scale=1.5):
    """绘制图像列表"""
    import matplotlib.pyplot as plt

    figsize = (num_cols * scale, num_rows * scale)
    _, axes = plt.subplots(num_rows, num_cols, figsize=figsize)
    axes = axes.flatten()
    for i, (ax, img) in enumerate(zip(axes, imgs)):
        if torch.is_tensor(img):
            # 图片张量
            ax.imshow(img.numpy())
        else:
            # PIL图片
            ax.imshow(img)
        ax.axes.get_xaxis().set_visible(False)
        ax.axes.get_yaxis().set_visible(False)
        if titles:
            ax.set_title(titles[i])
    plt.show()


def get_fashion_mnist_labels(labels):
    """返回Fashion-MNIST数据集的文本标签"""
    text_labels = ['t-shirt', 'trouser', 'pullover', 'dress', 'coat',
                   'sandal', 'shirt', 'sneaker', 'bag', 'ankle boot']
    return [text_labels[int(i)] for i in labels]


if __name__ == "__main__":
    mnist_train, mnist_test = download_dataset()
    print("Train dataset samples: ", len(mnist_train), "\nTest dataset samples:", len(mnist_test))

    X, y = next(iter(data.DataLoader(mnist_train, batch_size=18)))
    show_images(X.reshape(18, 28, 28), 2, 9, titles=get_fashion_mnist_labels(y))

看一看效果：

线性神经网络

# 线性回归

# 公式推导

# 损失函数

# 解析解

# 随机梯度下降

# 从零实现性线回归

# 准备数据集

# 实现代码

# 简化实现

# Softmax 回归

# 基础概念

# 损失函数

# 从零实现softmax回归

# 数据集准备

# 模型实现

线性回归

公式推导

损失函数

解析解

随机梯度下降

从零实现性线回归

准备数据集

实现代码

简化实现

Softmax 回归

基础概念

损失函数

从零实现softmax回归

数据集准备

模型实现