斯坦福机器学习笔记-第一周

这篇文章讲述机器学习的入门内容，是斯坦福大学吴恩达老师课程的笔记

什么是机器学习？

• Arthur Samuel(1959).Machine Learning:Field of study that gives computers the ability to learn without being explicitly programmed
• Tom Michell(1998). Well-posed Learning Problem:A computer program is said to learn from experience E with respect to some task T and some performance measure P,if its performance on T,as measured by P,improves with E.

什么是监督学习？

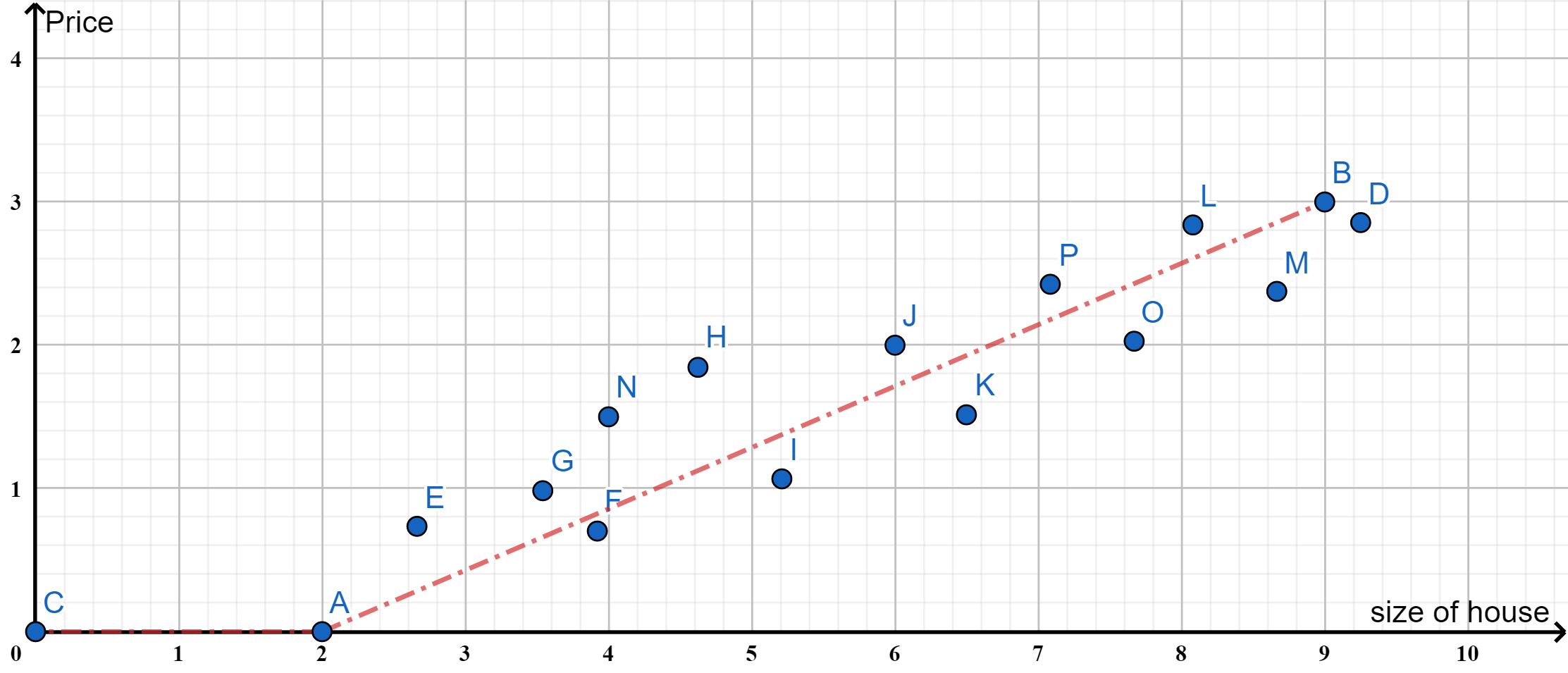
• 房价预测的例子

  给定一些房价跟其大小的数据，希望通过这些数据来预测新给定的房间（大小）的价格，这属于监督学习中的回归问题

  

• 肿瘤判别的例子

  给定一系列数据，希望通过肿瘤的大小判断肿瘤为良性或者恶性，这属于监督学习中的分类问题

  

• 多变量的分类问题

  上述肿瘤问题只涉及到一个变量，但是分类问题也可以有多个变量，比如肿瘤的良性（蓝色x）和恶性（红色O）不仅跟肿瘤大小相关，还跟患者的年龄有关，此时分类模型如下示意：

  

什么是无监督学习？

有监督学习将数据归类到其特定的类型，或者回归预测数据的趋势，而无监督学习则相反。对于某给定数据集，我们使用无监督学习去判断、归类数据的可能类别

无监督学习应用的例子：

• 计算机集群的组织
• 社交网络分析
• 市场细分
• 天文学数据分析

学习工具

快速的算法开发、验证工具：Octave

模型表示

使用$x^i$来表示第$i$个输入样本，使用$y^i$表示第$i$个输出，使用$h(\theta )$表示假设，其中$\theta$表示参数。

损失函数

对于一个线性回归问题，如下图：

我们给定一个假设函数$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$，期望找到对应的$\theta$参数使得拟合损失最小化：

$$minimize\{\frac{1}{2m}\sum _i^m[h_{\theta (x^i)}-y^i{]}^2\}$$

定义损失函数：$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}_i-y_i{)}^2$

为了理解损失函数$J(\theta )$与假设函数$h(x)$，观察以下示例：

对于不同的$\theta$值，期望找到使得$J(\theta )$最小的值，也即是上图中的${\theta }_0$

梯度下降

给定$J({\theta }_0,{\theta }_1)$，欲通过微调${\theta }_i$ 使得$J({\theta }_i)$ 达到最小值，如下图示意：

梯度下降示意

梯度下降的算法流程如下：

$${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)(forj=0,j=1)$$

上式中，$\alpha$代表学习率(learning rate)

例子：通过单参数的更新来了解梯度下降

梯度下降的更新过程

如上图：

a. 当初始点在极值左侧时，导数具有负的梯度，因此更新朝着右侧进行：$A->C->D->E->F->G->H$。

b. 当初始点在极值右侧时，导数具有正的梯度，更新朝着左侧进行：$B->I->J->K->L->H$。

c. $\alpha$ 控制了更新的幅度。越大的值更新幅度也越大。

线性回归的梯度下降

前面已经推导得到线性回归的损失函数：$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}_i-y_i{)}^2$

同理知道了梯度下降的更新公式：${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J({\theta }_0,{\theta }_1)(forj=0,j=1)$

将二者结合起来，可以获得线性回归的梯度下降更新公式：

$${\theta }_0:={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$$$${\theta }_1:={\theta }_1-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})$$